Til hvers lærum við eiginlega algebru?

„Ef þú kannt ekki skil á stærðfræði ertu að vissu leyti útilokaður frá mikilvægum þætti lýðræðissamfélagsins.“ Þetta segir Tomas Højgaard, prófessor í stærðfræðikennslu við Háskólann í Árósum.

Hann er hér á landi til að taka þátt í ráðstefnu um kennsluaðferðir, sem haldin er í dag í aðalsafni Borgarbókasafnsins við Tryggvagötu á vegum Landakotsskóla, Kvennaskólans og þjónustumiðstöðvar borgarinnar.

Tomas segir lýðræðisþáttinn vera eina mikilvægustu, og jafnframt vanmetnustu, réttlætinguna fyrir stærðfræðikennslu í grunn- og framhaldsskólum. „Samfélag okkar er svo tæknivætt og byggir að miklu leyti á stærðfræði,“ segir Tomas og nefnir tilhögun skatta, fjármál og hin ýmsu gögn sem verða á vegi fólks dag hvern.

Lýðræðissamfélag Norðurlanda treysti á hinn upplýsta og sjálfstæða einstakling, sem sé fær um að mynda sér skoðanir út frá upplýsingum sem hann afli sér. „Ef fólk skilur ekki stærðfræðina að baki er hætt við að það treysti sér ekki til að skipta sér af mikilvægum málum og hugsi að það verði einfaldlega að samþykkja það sem því er sagt.“

Tomas Højgaard og Ásdís Ingólfsdóttir, kennari í Kvennó, eru meðal þátttakenda á ráðstefnu sem ber nafnið Raddir nemenda og er lokahnykkurinn í tveggja ára samstarfsverkefni íslenskra, danskra og finnskra kennara á vegum Erasmus+, menntaáætlunar Evrópusambandsins. mbl.is/Kristinn Magnússon

Færa stærðfræði nær raunveruleikanum

Upp úr aldamótum skók slæm niðurstaða danskra nema í Pisa, samræmdu alþjóðlegu prófi OECD, danskan fræðaheim og stjórnmálastétt. Hvað olli því að danska skólakerfið, sem er með þeim best fjármögnuðu í heimi, stóð sig svo illa í að kenna börnum stærðfræði? Þessar spurningar hafa vafalaust hvarflað að mörgum Íslendingnum. Í kjölfarið var ráðist í gagngera endurskoðun á danskri námsskrá. Þá vinnu leiddi Tomas Højgaard og hefur sýn hans sett mark sitt á danska stærðfræðikennslu æ síðan.

Tomas segir að mikilvægt sé að sýna stærðfræðinemum að kennslan nýtist þeim í daglegu lífi, en sé ekki til þess eins fallin að hjálpa þeim á stærðfræðiprófi. Til þess þarf breyttar kennsluaðferðir og aukna áherslu á aðgerðagreiningu (e. mathematical modelling). Hann hefur sjálfur nýtt þessar aðferðir við kennslu og tekið upp óheyrilegan fjölda myndbanda úr kennslustofum, sem nálgast má á vefsvæði hans. Myndböndin eru læst vegna samkomulags við samstarfsaðila en hann hvetur áhugasama kennara til að hafa samband og fá hjá honum leyniorðið að myndböndunum, sem hann deilir einnig með blaðamanni.

Kennslunni er oft legið á hálsi fyrir að skorta tengingu við raunveruleikann. Nemendur verja drjúgum tíma í að þjálfa sig í tilteknum fyrirframgefnum aðferðum, svo sem að leysa ákveðnar gerðir af jöfnum, en oft gefst minna rými til að velta því fyrir sér til hvers leikurinn er gerður.

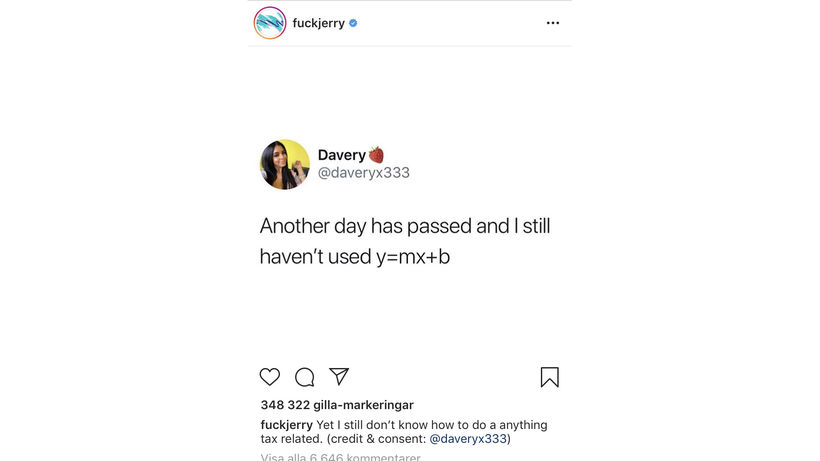
Umsjónarmenn Fuck Jerry, einnar vinsælustu „meme-síðu“ alnetsins virðast ekki hafa fundið góð not fyrir jöfnu línu. Fleiri deila þeirri skoðun. Skjáskot/Instagram

„Það er til lítils að kunna að leysa jöfnur ef maður getur ekki sett þær fram til að byrja með þegar maður stendur frammi fyrir raunverulegum verkefnum,“ segir Tomas. Hann hefur um árabil kennt kennaranemum sem hyggjast leggja fyrir sig stærðfræðikennslu, og auk þess unnið verkefni með nemendum bæði í grunn- og framhaldsskólum.

„Skilaboð mín til kennara eru einföld: Við verðum að kenna það sem við viljum að nemendur læri,“ segir Tomas. Það sé þó ein stærsta uppgötvun í stærðfræðikennslu síðustu áratuga.

Fyrri hugmyndir gengu út á að ef nemendum væru kenndar aðferðir í reikningi og hvernig leysa á jöfnur, þá kæmi annað af sjálfu sér. „En það er aðeins í skólastofu sem fólk fær fullbúnar jöfnur upp í hendurnar.“

Tomas segir að vitanlega þurfi að kenna hefðbundnar aðferðir í stærðfræðitímum, en jafnframt að veita nemendum ákveðið frelsi til þess að nýta sér þekkingu sína á fjölbreyttari hátt. Ekki bara til að leysa uppsett dæmi með aðferðinni sem kennd var á síðustu blaðsíðu kennslubókarinnar.

Svona gæti hefðbundið stærðfræðidæmi á efri árum grunnskólans litið út:
Í einni túbu af tannkremi eru 100 millilítrar. Við hverja tannburstun þarf hálfan millilítra af tannkremi. Jón, Sara og börnin þeirra tvö bursta öll tvisvar á dag. Hve margar tannkremstúbur notar fjölskyldan á ári?

Raunveruleikinn er hins vegar sjaldnast svo klipptur og skorinn. Tomas hefur sett fram hugmyndir um hvernig má þjálfa nemendur í að ræða saman um stærðfræði og setja sjálf fram formúlur um margs konar þætti í umhverfi og samfélagi.

Þannig mætti varpa fram spurningunni: Hvað haldið þið að fjölskylda noti margar tannkremstúbur á ári?

Nemendur ræða málin og átta sig þar með á þeim ýmsu breytum sem innifaldar eru í dæminu. Hvað er fjölskyldan stór? Hver er stærð tannkremstúbu? Hversu oft bursta þau tennurnar og hvað notar fólk eiginlega mikið tannkrem við hverja tannburstun?

Forsendurnar sjálfar skipta ekki höfuðmáli, einungis að nemendur átti sig á samspili breytanna og niðurstöðunnar. Eftir töluverðar umræður fæst út að fjöldi túba sem fjölskyldan notar á ári (y) má lýsa með jöfnunni:
y = 365*æ*t*m/s

þar sem æ táknar fjölda heimilismanna, t táknar fjölda tannburstana hvers fjölskyldumeðlims á dag, m táknar magnið af tannkremi sem notað er við hverja burstun og s táknar stærð túbunnar. Miðað við upphaflegar forsendur er svarið 14,6 en lesendur geta skemmt sér við að stinga viðeigandi gildum inn fyrir breyturnar og reikna þannig út eigin tannkremsnotkun.

Hann viðurkennir að þessi aðferð sé strembnari og sennilega eigi það sinn þátt í því hve ríkjandi hefðbundnar kennsluaðferðir eru um allan heim. „Þegar hefðbundnar aðferðir við útreikninga eru kenndar er kennarinn óumdeildur sérfræðingur og líkurnar á því að nemendur komi honum í opna skjöldu og geri eitthvað óvænt eru litlar,“ segir Tomas.

Ef nemendum er hins vegar sagt að koma upp með eigin aðferðir til að leysa dæmi og kennarinn muni leiðbeina þeim í gegnum útreikningana er hættan að nemendur fari ólíkar og óvæntar leiðir, og kennarinn þurfi að vera undir það búinn að setja sig hratt inn í aðstæður. „Þetta er vissulega krefjandi fyrir stærðfræðikennara því þeir eru ekki vanir þessu.“

Aldrei má gleyma upprunanum

Tomas segir mikilvægt að spyrja gagnrýnna spurninga, svo sem hvers vegna börn séu látin læra stærðfræði. „Stærðfræði er sennilega sú námsgrein sem mest er kennd á alþjóðagrundvelli. Um heim allan sitja börn stærðfræðitíma nær daglega allan grunnskólann. Ef við vitum ekki hvers vegna við stöndum í þessu er hætt við að kennslan verði marklaus og nemendur óáhugasamir.“

Auk lýðræðisvinkilsins nefnir Tomas að starfshæfni sé jafnan fyrst nefnd sem ástæða stærðfræðikennslu. Með góðum undirbúningi í stærðfræði á yngri árum gefst kostur á frekara námi í raungreinum í háskóla, sem síðan má nýta í hin ýmsu verðmætaskapandi störf í tæknigeiranum, bönkum og víðar. Lesendur kippast sennilega ekki til í sætinu við þessi sannindi.

Ekki má þó síður gleyma áhrifum stærðfræðikunnáttu á einstaklinginn sjálfan, segir Tomas. „Stærðfræðiþekking gerir menn betri í að standa á eigin fótum, skilja umheiminn og draga ályktanir út frá gagnasöfnum og upplýsingum,“ segir Tomas, já og skilja hvernig skatturinn manns er reiknaður. Honum er, eins og sönnum Dana sæmir, tíðrætt um skatta og hlutverk þeirra sem undirstöðu velferðarsamfélagsins.

„Það er mikilvægt að koma nemendum í skilning um ástæður stærðfræðikennslu,“ segir Tomas. Í stað þess að segja þeim einfaldlega að þau skuli læra þetta og hitt verði að fræða þau um gagnsemi þess sem skal kenna og hvernig það nýtist þeim í daglegu lífi.

4,7 túbur á ári reiknast blaðamanni til að heimili hans, sem samanstendur af honum einum, noti af tannkremi á ári. mbl.is/Jim Smart

• Blogga um frétt